激活函数
加入非线性因素,解决线性模型缺陷
激活函数的主要作用是提供网络的非线性建模能力。如果没有激活函数,那么该网络仅能够表达线性映射,此时即便有再多的隐藏层,其整个网络跟单层神经网络也是等价的。因此也可以认为,只有加入了激活函数之后,深度神经网络才具备了分层的非线性映射学习能力。
如果没有激活函数会怎么样?
对于y=ax+b 这样的函数,当x的输入很大时,y的输出也是无限大小的,经过多层网络叠加后,值更加膨胀的没边了,这显然不符合我们的预期,很多情况下我们希望的输出是一个概率
线性的表达能力太有限了,即使经过多层网络的叠加,y=ax+b无论叠加多少层最后仍然是线性的,增加网络的深度根本没有意义。线性回归连下面这个最简单的“异或”x1 XOR x2,都无法拟合:
因为神经网络的数学基础是处处可微的,所以选取的激活函数要能保证数据输入与输出也是可微的。在神经网络里常用的激活函数有Sigmoid、Tanh和relu等,下面逐一介绍。
Sigmoid函数
Sigmoid是常见的激活函数,一起看看它的样子。
1). 函数介绍
Sigmoid是常用的非线性的激活函数,其数学形式。
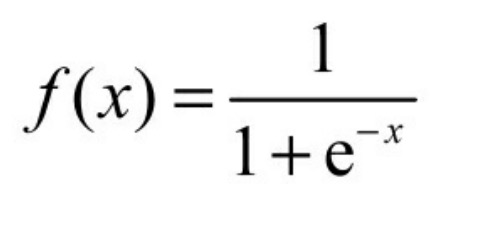
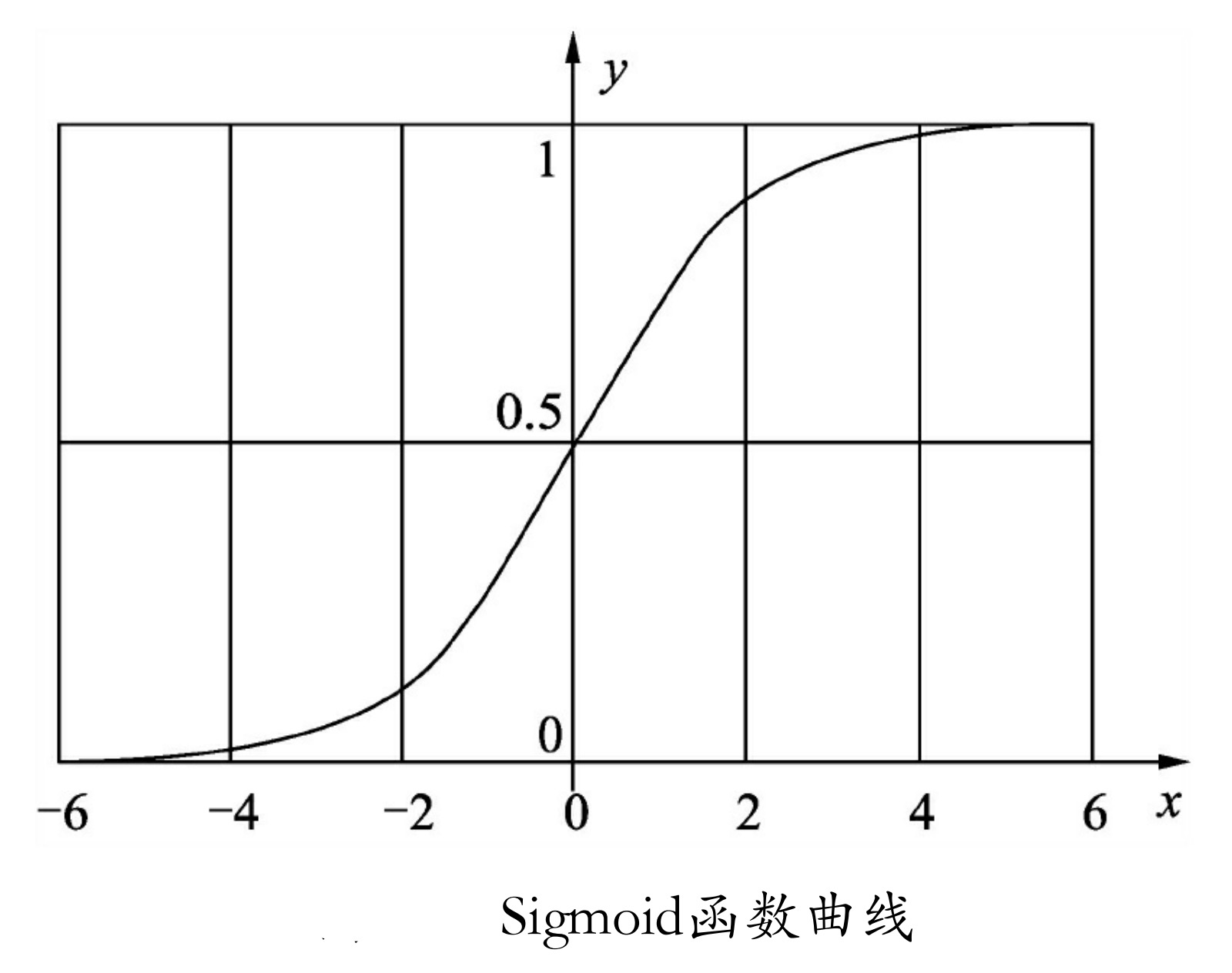
Sigmoid函数曲线如图所示,其中,x可以是正无穷到负无穷,但是对应的y却只有0~1的范围,所以,经过Sigmoid函数输出的函数都会落在0~1的区间里,即Sigmoid函数能够把输入的值“压缩”到0~1之间。
2). 在TensorFlow中对应的函数
tf.nn.sigmoid(x, name=None)
从图像上看,随着x趋近正负无穷大,y对应的值越来越接近1或-1,这种情况叫做饱和。处于饱和态的激活函数意味着,当x=100和x=1000时的反映都是一样的,这样的特性转换相当于将1000大于100十倍这个信息给丢失了。
所以,为了能有效使用Sigmoid函数,从图中看其极限也只能是-6~6之间,而在-3~3之间应该会有比较好的效果。
Tanh函数
Tanh函数可以说是Sigmoid函数的值域升级版,由Sigmoid函数的0~1之间升级到-1~1。但是Tanh函数也不能完全替代Sigmoid函数,在某些输出需要大于0的情况下,还是要用Sigmoid函数。
1). 函数介绍
Tanh函数也是常用的非线性激活函数,其数学形式。
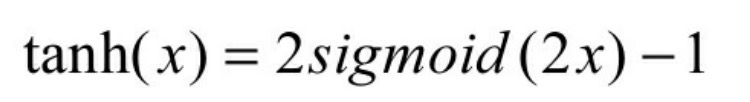
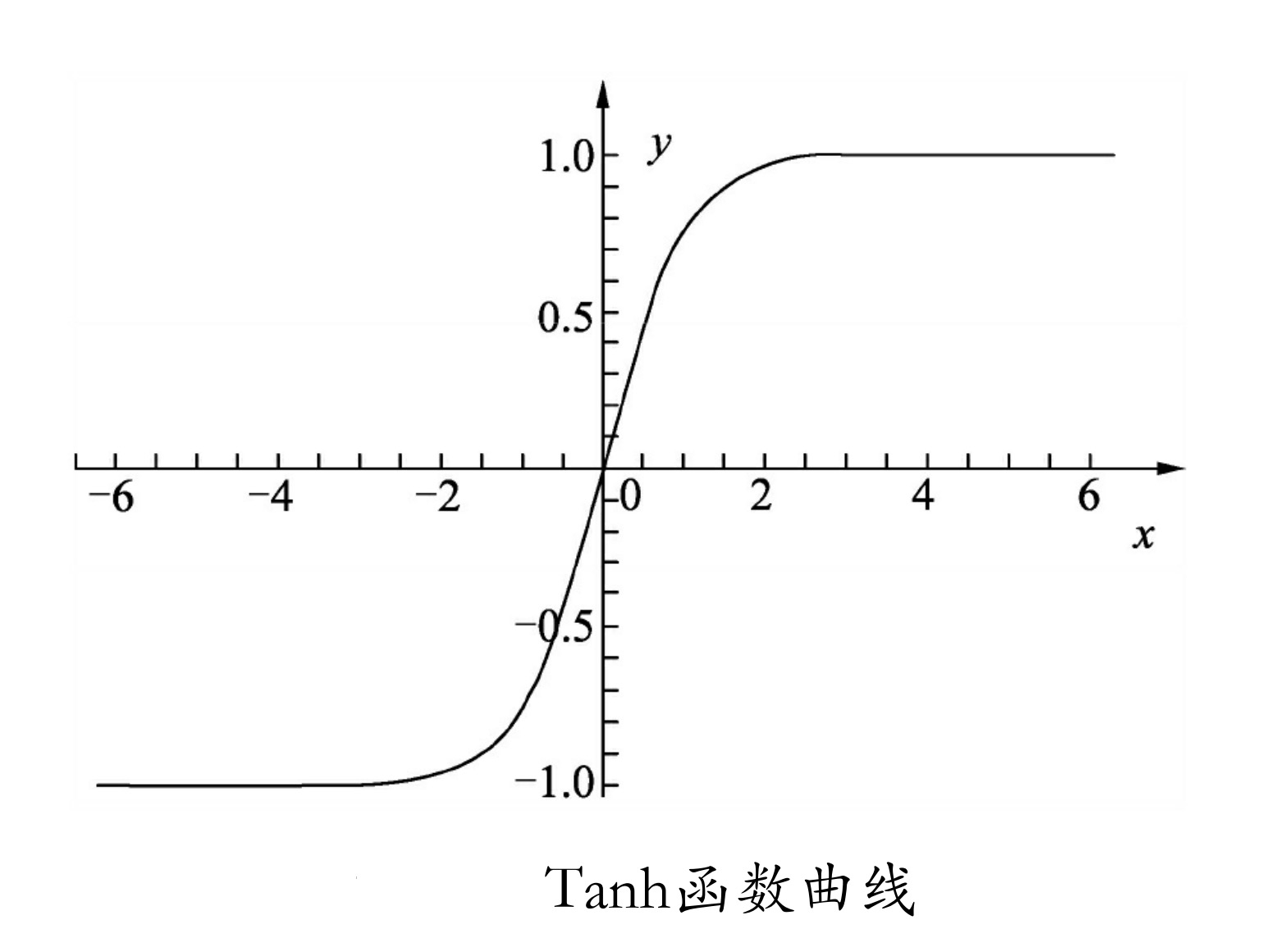
Tanh函数曲线如图所示,其x取值也是从正无穷到负无穷,对应的y值变为-1~1之间,相对于Sigmoid函数有更广的值域。
2).在TensorFlow中对应的函数
tf.nn.tanh(x, name=None)
显而易见,Tanh函数跟Sigmoid函数有一样的缺陷,也是饱和问题,所以在使用Tanh函数时,要注意输入值的绝对值不能过大,否则模型无法训练。
ReLU函数
1). 函数介绍
除了前面介绍的Sigmoid函数和Tanh函数之外,还有一个更为常用的激活函数(也称为Rectifier)。其数学形式见式。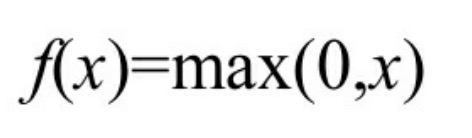
该式非常简单,大于0的留下,否则一律为0,具体的图像如图所示。ReLU函数应用的广泛性与它的优势是分不开的,这种对正向信号的重视,忽略了负向信号的特性,与我们人类神经元细胞对信号的反映极其相似。所以在神经网络中取得了很好的拟合效果。
另外由于ReLU函数运算简单,大大地提升了机器的运行效率,也是Relu函数一个很大的优点。
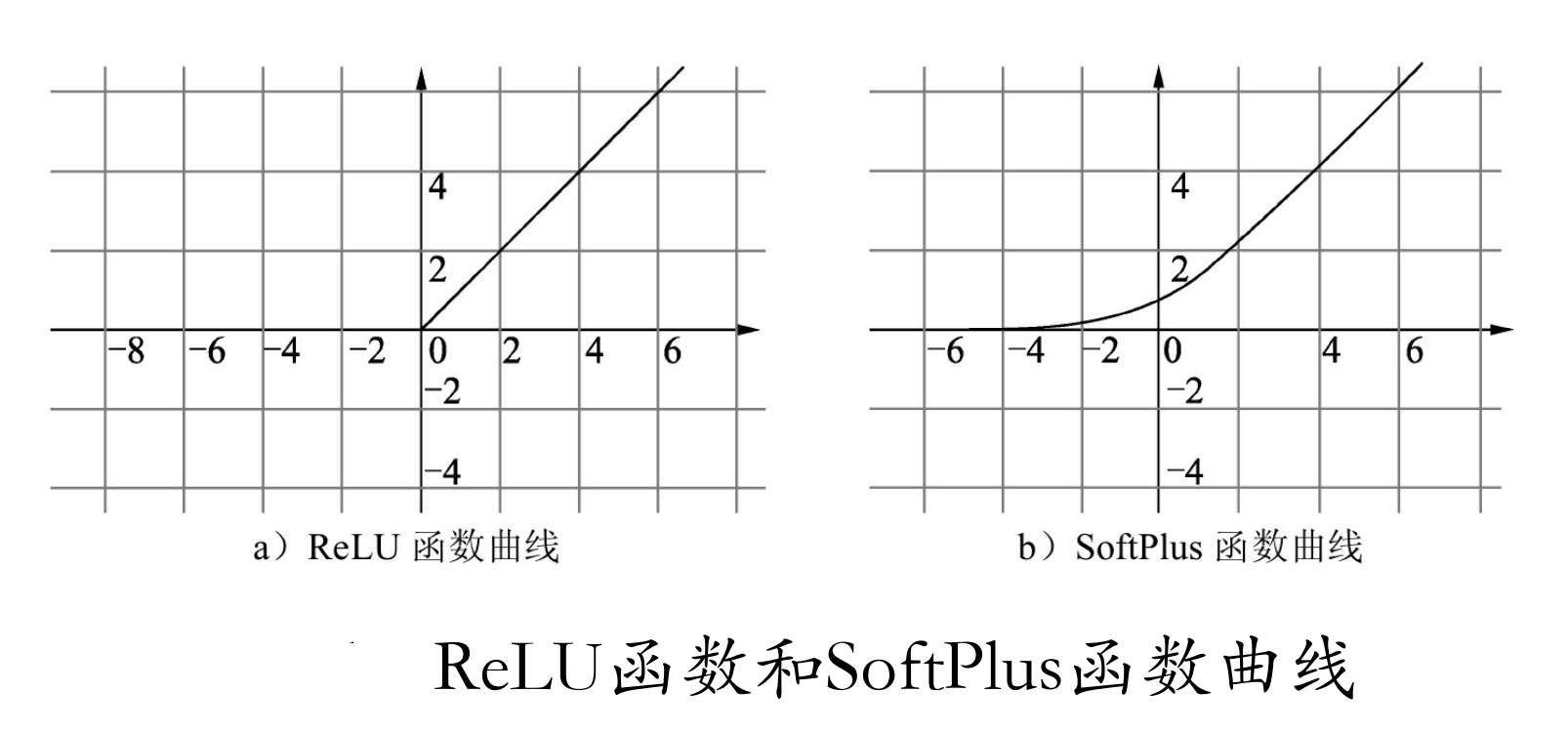
与ReLU函数类似的还有Softplus函数,如图所示。二者的区别在于:Softplus函数会更加平滑,但是计算量很大,而且对于小于0的值保留的相对更多一点。Softplus函数公式见式。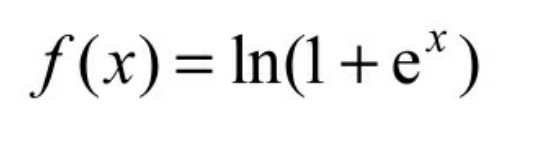
虽然ReLU函数在信号响应上有很多优势,但这仅仅在正向传播方面。由于其对负值的全部舍去,因此很容易使模型输出全零从而无法再进行训练。例如,随机初始化的w加入值中有个值是负值,其对应的正值输入值特征也就被全部屏蔽了,同理,对应负值输入值反而被激活了。这显然不是我们想要的结果。于是在基于ReLU的基础上又演化出了一些变种函数,举例如下:
- Noisy relus:为max中的x加了一个高斯分布的噪声,见式。

- Leaky relus:在ReLU基础上,保留一部分负值,让x为负时乘0.01,即Leaky relus对负信号不是一味地拒绝,而是缩小。其数学形式见式。
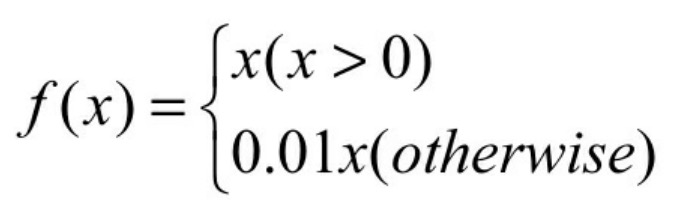
- 再进一步让这个0.01作为参数可调,于是,当x小于0时,乘以a,a小于等于1。其数学形式见式。
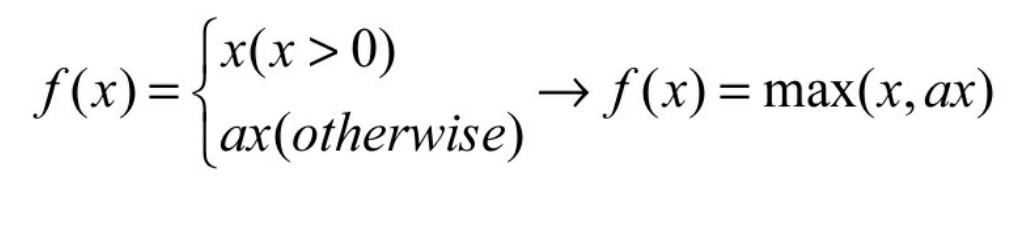
得到Leaky relus的公式max(x,ax) - Elus:当x小于0时,做了更复杂的变换,见式(6-9)。
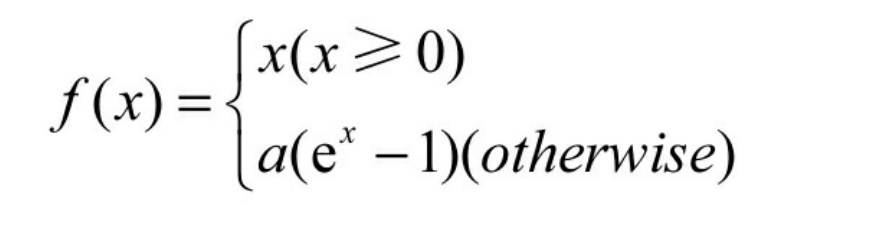
Elus函数激活函数与ReLU函数一样都是不带参数的,而且收敛速度比ReLU函数更快,使用Elus函数时,不使用批处理比使用批处理能够获得更好的效果,同时Elus函数不使用批处理的效果比ReLU函数加批处理的效果要好。
2).在TensorFlow中对应的函数
在TensorFlow中,关于ReLU函数的实现,有以下两个对应的函数:
- tf.nn.relu(features,name=None) :是一般的ReLU函数,即max(features,0);
- tf.nn.relu6(features,name=None):是以6为阈值的ReLU函数,即min(max(features,0),6)。
注意: relu6存在的原因是防止梯度爆炸,当节点和层数特别多而且输出都为正时,它们的加和会是一个很大的值,尤其在经历几层变换之后,最终的值可能会离目标值相差太远。误差太大,会导致对参数调整修正值过大,这会导致网络抖动得较厉害,最终很难收敛。
在TensorFlow中,Softplus函数对应的函数如下:
tf.nn.softplus(features, name=None);
在TensorFlow中,Elus函数对应的函数如下:
tf.nn.elu(features, name=None)
在TensorFlow中,Leaky relus公式没有专门的函数,不过可以利用现有函数组成而得到:
tf.maximum(x, leak*x, name = name) #leak 为传入的参数,可以设为0.01 等
Swish函数
Swish函数是谷歌公司发现的一个效果更优于Relu的激活函数。经过测试,在保持所有的模型参数不变的情况下,只是把原来模型中的 ReLU激活函数修改为 Swish 激活函数,模型的准确率均有提升。其公式
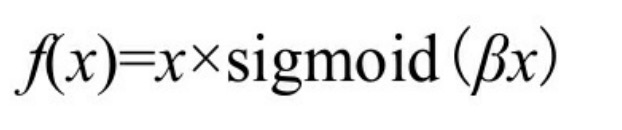
其中β为x的缩放参数,一般情况取默认值1即可。在使用了BN算法(见8.9.3节)的情况下,还需要对x的缩放值β进行调节。
在TensorFlow的低版本中,没有单独的Swish函数,可以手动封装,代码如下:
def Swish(x,beta=1):
return x * tf.nn.sigmoid(x*beta)
2.5 激活函数总结
神经网络中,运算特征是不断进行循环计算,所以在每代循环过程中,每个神经元的值也是在不断变化的。这就导致了Tanh函数在特征相差明显时的效果会很好,在循环过程中其会不断扩大特征效果并显示出来。
但有时当计算的特征间的相差虽比较复杂却没有明显区别,或是特证间的相差不是特别大时,就需要更细微的分类判断,这时Sigmoid函数的效果就会更好一些。
后来出现的ReLU激活函数的优势是,经过其处理后的数据有更好的稀疏性。即,将数据转化为只有最大数值,其他都为0。这种变换可以近似程度地最大保留数据特征,用大多数元素为0的稀疏矩阵来实现。
实际上,神经网络在不断反复计算中,就变成了ReLU函数在不断尝试如何用一个大多数为0的矩阵来表达数据特征。以稀疏性数据来表达原有数据特征的方法,使得神经网络在迭代运算中能够取得又快又好的效果,所以目前大多max(0,x)来代替Sigmod函数。


