softmax算法

处理分类问题

softmax基本上可以算是分类任务的标配。在本节中需要学会softmax为什么能分类，以及如何使用softmax来分类。如果需要比较哪个更重要，当然是学会如何使用会更重要。

什么是softmax

对于前面讲的激活函数，其输出值只有两种（0、1，或-1、1，或0、x），而现实生活中需要对某一问题进行多种分类，例如前面的图片分类例子，这时就需要使用softmax算法。

softmax，看名字就知道，就是如果判断输入属于某一个类的概率大于属于其他类的概率，那么这个类对应的值就逼近于1，其他类的值就逼近于0。

该算法的主要应用就是多分类，而且是互斥的，即只属于其中的一个类。与sigmoid类的激活函数不同的是，一般的激活函数只能分两类，所以可以理解成Softmax是Sigmoid类的激活函数的扩展，其算法如下。

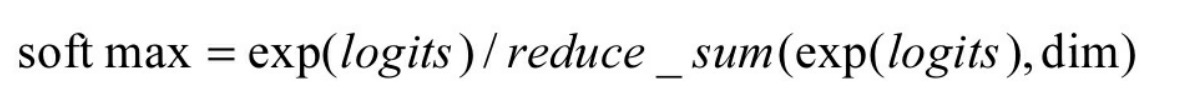
把所有值用e的n次方计算出来，求和后算每个值占的比率，保证总和为1，一般就可以认为softmax得出的就是概率。这里的exp（logits）指的就是elogits。

注意： 对于要生成的多个类任务中不是互斥关系的任务，一般会使用多个二分类来组成。

softmax原理

softmax原理很简单，如图所示为一个简单的Softmax网络模型，输入X1 和X2 ，要准备生成Y1 、Y2 和Y3 三个类。

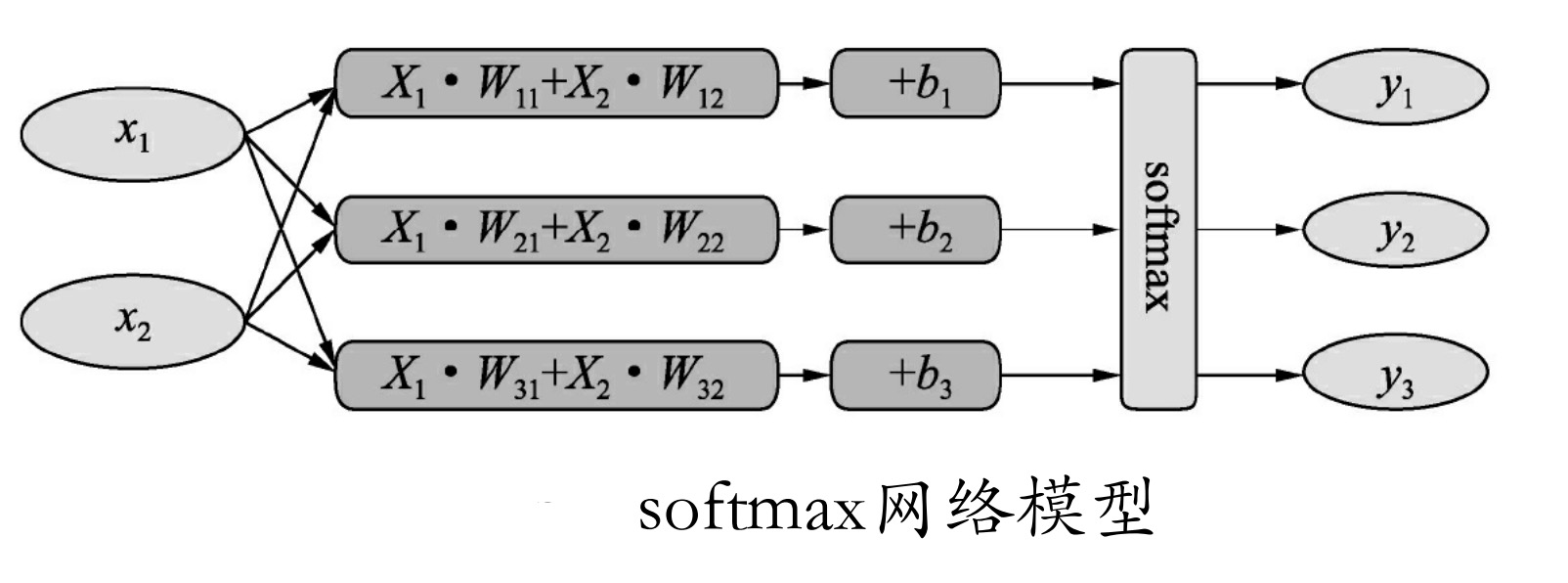
对于属于y1 类的概率，可以转化成输入x1 满足某个条件的概率，与x2 满足某个条件的概率的乘积。

在网络模型里把等式两边都取ln。这样，ln后的属于y1类的概率就可以转化成，ln后的x1 满足某个条件的概率加上ln后的x2 满足某个条件的概率。这样y1 =x1 w11 +x2 w12 =ln后y1的概率了。这也是softmax公式中要进行一次e的logits次方的原因。

注意： 等式两边取ln是神经网络中常用的技巧，主要用来将概率的乘法转变成加法，即ln（x*y）=lnx+lny。然后在后续计算中再将其转为e的x次方，还原成原来的值。

了解完e的n次方的意义后，softmax就变得简单至极了。

举例：

某个样本经过生成的值y1为5，y2为3，y3为2。那么对应的概率就为y1=5/10=0.5，y2=3/10，y3=2/10，于是取最大的值y1为最终的分类。

softmax在机器学习中有非常广泛的应用，前面介绍过MNIST的每一张图片都表示一个数字，从0到9。我们希望得到给定图片代表每个数字的概率。

例如，训练的模型可能推测一张包含9的图片代表数字9的概率是80%，但是判断它是8的概率是5%（因为8和9都有上半部分相似的小圆），判断它代表其他数字的概率值更小。于是取最大概率的对应数值，就是这个图片的分类了。这是一个使用softmax回归（softmax regression）模型的经典案例。

注意： 在实际使用中，softmax伴随的分类标签都为one_hot编码，而且这里还有个小技巧，在softmax时需要将目标分成几类，就在最后这层放几个节点。

常用的分类函数