单个神经元
从现在开始,我们将真正进入深度学习理论知识系统。神经网络是由多个神经元组成,所以本章先从一个神经元开始讲起。一个神经元由以下几个关键知识点组成:
- 激活函数
- 损失函数
- 梯度下降
神经元的拟合原理
在前面“MNIST分类.py”中,建立的模型是一个单个神经元组成的网络模型。单个神经元的网络模型如图所示。
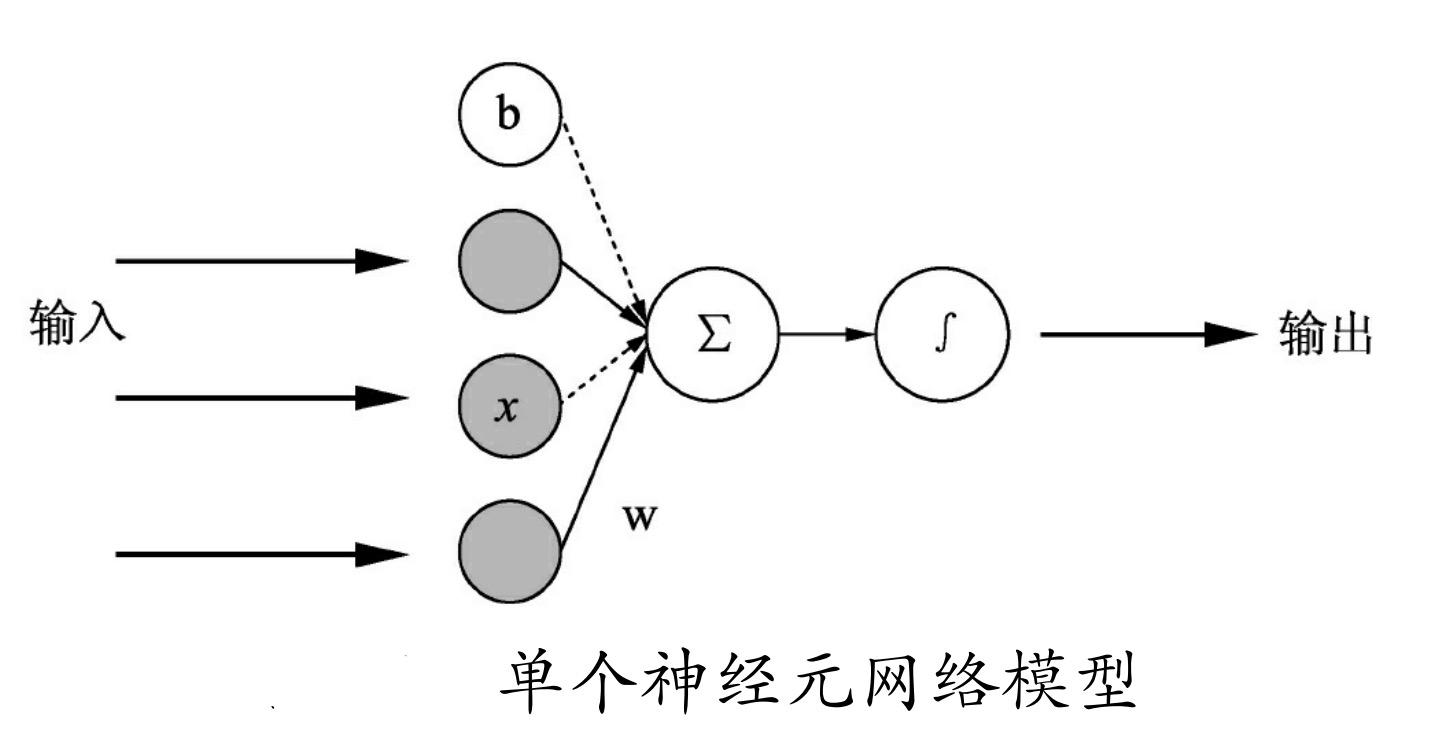
其计算公式
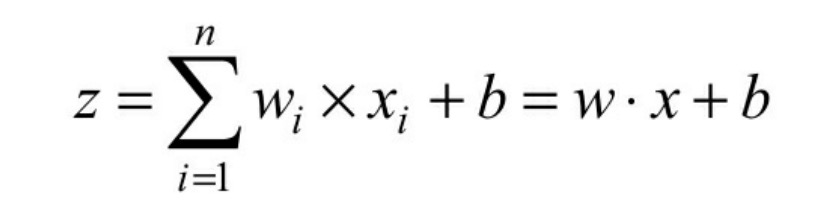
式中:z为输出的结果;x为输入;w为权重;b为偏执值。w和b可以理解为两个变量。
模型每次的学习都是为了调整w和b从而得到一个合适的值,最终由这个值配合运算公式所形成的逻辑就是神经网络的模型。
其实这个模型是根据仿生学得来的。我们看一下大脑细胞里的神经突出如图所示。
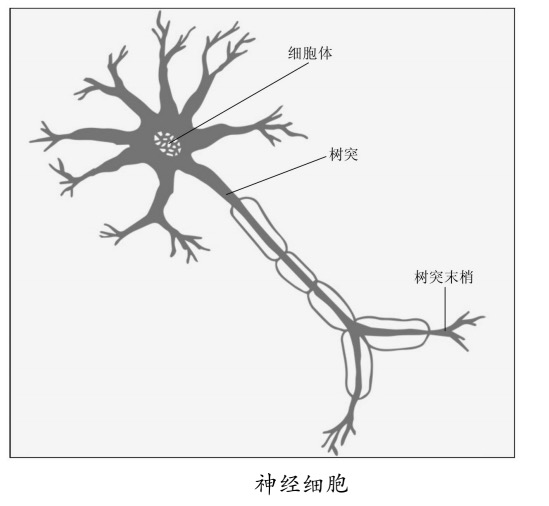
是不是与我们建立的模型有点神似?
大脑神经细胞是靠生物电来传递信号的,可以理解成经过模型里的具体数值。
仔细观察发现神经细胞相连的连接树突有粗有细,显然通过不同粗细连接的生物电信号,也会有不同的影响。这就好比权重w,因为每个输入节点都会与相关连接的w相乘,也就实现了对信号的放大、缩小处理。
这里唯独不透明的就是中间的细胞体,于是我们将
所有输入的信号经过w变换之后,再添加一个额外的偏执量b,把它们加在一起求合,然后再选择一个模拟细胞体处理的函数来实现整个过程的仿真。这个函数称其为激活函数。
我们把w和b赋予合适的值时,再配合合适的激活函数,就会发现它可以产生很好的拟合效果。
1.1 正向传播
前文描述的过程过程叫做正向传播,数据是从输入到输出的流向传递过来的。当然,它是在一个假设有合适的w和b的基础上,才可以实现对现实环境的正确拟合。但是,在实际过程中我们无法得知w和b的值具体是多少才算是正常的。于是我们加入了一个训练过程,通过反向误差传递的方法让模型自动来修正,最终产生一个合适的权重。
1.2 反向传播
反向传播的意义很明确——告诉模型我们需要将w和b调整到多少。在刚开始没有得到合适的权重时,正向传播生成的结果与实际的标签是有误差的,反向传播就是要把这个误差传递给权重,让权重做适当地调整来达到一个合适的输出。
在实际训练过程中,很难一次将其调整到位,而是通过多次迭代一点一点的将其修正,最终直到模型的输出值与实际标签值的误差小于某个阀值为止。
如何将输出的误差转化为权重的误差,这里面使用的就是BP算法。
BP算法介绍
不阐述过多的算法,只讲原理,理解道理即可。
BP算法(back propagation)又称“误差反向传播算法”。我们最终的目的,是要让正向传播的输出结果与标签间的误差最小化,这就是反向传播的核心思想。
正向传播的模型是清晰的,所以很容易得出一个关于由b和w组成的对于输出的表达式。接着,也可以得出一个描述损失值的表达式(将输出值与标签直接相减,或是做平方差等运算)。
为了要让这个损失值变得最小化,我们运用数学知识,选择一个损失值的表达式让这个表达式有最小值,接着通过对其求导的方式,找到最小值时刻的函数切线斜率(也就是梯度),从而让w和b的值沿着这个梯度来调整。
至于每次调整多少,我们引入一个叫做“学习率”的参数来控制,这样通过不断的迭代,使误差逐步接近最小值,最终达到我们的目标。


