现在有一个场景:
Alice想要用私钥签名一个数据,Bob想要使用Alice的公钥验证这个签名;只有Alice能够进行计算签名然后得到签名,每个人都能验证签名值。
首先Alice和Bob拥有相同的椭圆曲线参数,算法被签名称之为ECDSA,是DSA算法的一个变体。
ECDSA签名算法的输入是数据的哈希值,而不是数据的本身,至于哈希算法选用哪一个就取决于自己了。为了使得ECDSA的输入值的比特数和子群的阶n的比特数一样,哈希值可能会被截断。我们把ECDSA输入称之为Z。
算法工作流程如下:
(1)取一个范围在[1, n - 1]的随机数k
(2)计算点P=kG
(3)计算r = xp mod n
(4)如果 r == 0,执行第一步
(5)计算s = k^-1 (z + r*da) mod n (da是Alice的公钥,k^-1 是 k 对n的逆元)
(6)如果s==0,执行第一步
(7)二元组(r, s)就是签名值
(一般情况,最后的结果r和s是用asn1格式封装的,至少的TLS签名和数字证书签名中是这样的,不是简单的r+s这样字节直接拼接)
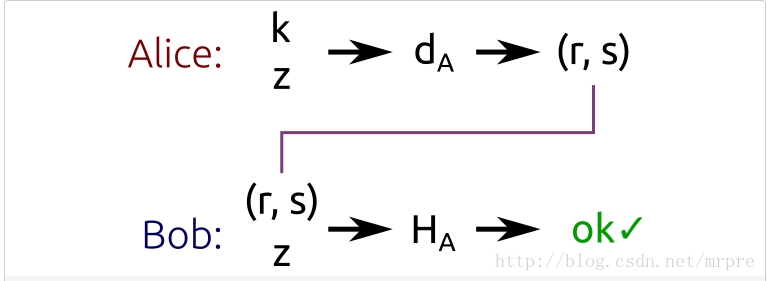
上图中,Alice使用私钥da对z进行签名,生成二元组(r, s)。
Bob使用Alice的公钥对(r, s)和Z进行验证,我们来看看Bob如何验证的:
(1)计算u1 = s^-1 z mod n
(2)计算u2 = s^-1 r mod n
(3)计算P = u1G + u2Ha
(4)如果r == xp mod n,则验证正确
ECDSA原理以及证明
首先,我们计算了P = u1G + u2Ha
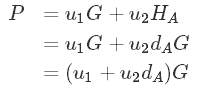
代入u1、u2
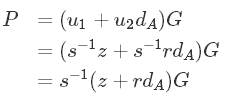
我们得到这个等式。
然后再看看这个等式:
s = k^-1 (z + r*da) mod n
两边乘以(s^-1 k)
得到 等式 k = s^-1 (z + rda) mod n
两边再乘以G,得到
kG = s^-1*(z + r *da)*G mod n = P
换句话说,如果(r,s)是有客户端私钥签名Z得到,则我们通过u1,u2计算的到的P值得x分量和r相同。
K的重要性
当我们使用ECDSA进行签名的时候,k的保密性非常重要。如果我们对所以的签名操作都用一样的k或者我们的随机数生成器存在可预测性,一个攻击者可能会猜出私钥。
索尼几年前曾犯过这个错误。PlayStation 3 只能运行被索尼的进行ECDSA签名的游戏。如果我想为PlayStation 3开发了一个新的游戏,除非我从索尼获得签名值,否则我及时发布了,也运行不了这个游戏。问题是,索尼签名时用了一个静态的k值而不是随机生成的。
这么获取私钥d和随机数k?
看看这个等式 s = k^-1 (z + r*da) mod n
显然,未知数只有2个,da和k。我们买2份索尼游戏,签名值分别是(r1 , s1)、(r2, s2), 由于k值一样,故r 值也一样
s1 = k^-1 (z1 + r*da) mod n等式1
s2= k^-1 (z2 + r*da) mod n等式2
等式1-等式2
s1 -s2 = k^-1 (z1 - z2) mod n
z1和z2 可以自己使用哈希算法对软件进行哈希能够获取到。s1和s2能够从前面值中获取到。所以k值就轻松的获取到了
K = (s1 -s2)^-1 * (z1 -z2) mod n
再把k值代入等式1或者等式2,就能计算da了。


