如何理解函数式编程

编程范式

函数式编程是一种编程范式，我们常见的编程范式有命令式编程（Imperative programming），函数式编程，逻辑式编程，常见的面向对象编程是也是一种命令式编程。

命令式编程是面向计算机硬件的抽象，有变量（对应着存储单元），赋值语句（获取，存储指令），表达式（内存引用和算术运算）和控制语句（跳转指令），一句话，命令式程序就是一个冯诺依曼机的指令序列。

而函数式编程是面向数学的抽象，将计算描述为一种表达式求值，一句话，函数式程序就是一个表达式。

函数式编程的本质

函数式编程中的函数这个术语不是指计算机中的函数（实际上是Subroutine），而是指数学中的函数，即自变量的映射。也就是说一个函数的值仅决定于函数参数的值，不依赖其他状态。比如sqrt(x)函数计算x的平方根，只要x不变，不论什么时候调用，调用几次，值都是不变的。

在函数式语言中，函数作为一等公民，可以在任何地方定义，在函数内或函数外，可以作为函数的参数和返回值，可以对函数进行组合。

纯函数式编程语言中的变量也不是命令式编程语言中的变量，即存储状态的单元，而是代数中的变量，即一个值的名称。变量的值是不可变的（immutable），也就是说不允许像命令式编程语言中那样多次给一个变量赋值。比如说在命令式编程语言我们写“x = x + 1”，这依赖可变状态的事实，拿给程序员看说是对的，但拿给数学家看，却被认为这个等式为假。

函数式语言的如条件语句，循环语句也不是命令式编程语言中的控制语句，而是函数的语法糖，比如在Scala语言中，if else不是语句而是三元运算符，是有返回值的。

严格意义上的函数式编程意味着不使用可变的变量，赋值，循环和其他命令式控制结构进行编程。

从理论上说，函数式语言也不是通过冯诺伊曼体系结构的机器上运行的，而是通过λ演算来运行的，就是通过变量替换的方式进行，变量替换为其值或表达式，函数也替换为其表达式，并根据运算符进行计算。λ演算是图灵完全（Turing completeness）的，但是大多数情况，函数式程序还是被编译成（冯诺依曼机的）机器语言的指令执行的。

函数式编程的好处

由于命令式编程语言也可以通过类似函数指针的方式来实现高阶函数，函数式的最主要的好处主要是不可变性带来的。没有可变的状态，函数就是引用透明（Referential transparency）的和没有副作用（No Side Effect）。

一个好处是，函数即不依赖外部的状态也不修改外部的状态，函数调用的结果不依赖调用的时间和位置，这样写的代码容易进行推理，不容易出错。这使得单元测试和调试都更容易。

不变性带来的另一个好处是：由于（多个线程之间）不共享状态，不会造成资源争用(Race condition)，也就不需要用锁来保护可变状态，也就不会出现死锁，这样可以更好地并发起来，尤其是在对称多处理器（SMP）架构下能够更好地利用多个处理器（核）提供的并行处理能力。

2005年以来，计算机计算能力的增长已经不依赖CPU主频的增长，而是依赖CPU核数的增多，如图：

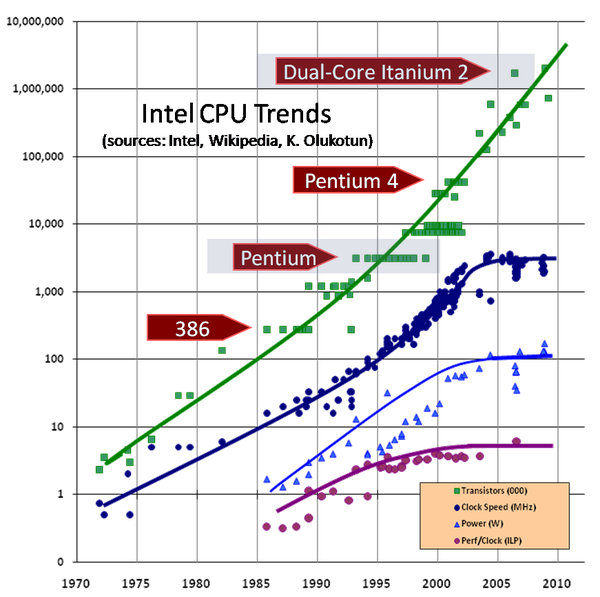
（图片来源：（图片来源：The Free Lunch Is Over: A Fundamental Turn Toward Concurrency in Software ）

图中深蓝色的曲线是时钟周期的增长，可以看到从2005年前已经趋于平缓。 在多核或多处理器的环境下的程序设计是很困难的，难点就是在于共享的可变状态。在这一背景下，这个好处就有非常重要的意义。

由于函数是引用透明的，以及函数式编程不像命令式编程那样关注执行步骤，这个系统提供了优化函数式程序的空间，包括惰性求值和并性处理。

还有一个好处是，由于函数式语言是面向数学的抽象，更接近人的语言，而不是机器语言，代码会比较简洁，也更容易被理解。

函数式编程的特性
由于变量值是不可变的，对于值的操作并不是修改原来的值，而是修改新产生的值，原来的值保持不便。例如一个Point类，其moveBy方法不是改变已有Point实例的x和y坐标值，而是返回一个新的Point实例。

class Point(x: Int, y: Int){
    override def toString() = "Point (" + x + ", " + y + ")"

    def moveBy(deltaX: Int, deltaY: Int) = {
        new Point(x + deltaX, y + deltaY)
    }
}

（示例来源：Anders Hejlsberg在echDays 2010上的演讲）

同样由于变量不可变，纯函数编程语言无法实现循环，这是因为For循环使用可变的状态作为计数器，而While循环或DoWhile循环需要可变的状态作为跳出循环的条件。因此在函数式语言里就只能使用递归来解决迭代问题，这使得函数式编程严重依赖递归。

通常来说，算法都有递推（iterative）和递归（recursive）两种定义，以阶乘为例，阶乘的递推定义为：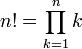

而阶乘的递归定义

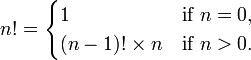
递推定义的计算时需要使用一个累积器保存每个迭代的中间计算结果，Java代码如下：递推定义的计算时需要使用一个累积器保存每个迭代的中间计算结果，Java代码如下：

public static int fact(int n){
  int acc = 1;

  for(int k = 1; k <= n; k++){
    acc = acc * k;
  }

  return acc;
}

而递归定义的计算的Scala代码如下：

def fact(n: Int):Int= {
  if(n == 0) return 1
  n * fact(n-1)
}

我们可以看到，没有使用循环，没有使用可变的状态，函数更短小，不需要显示地使用累积器保存中间计算结果，而是使用参数n（在栈上分配）来保存中间计算结果。

当然，这样的递归调用有更高的开销和局限（调用栈深度），那么尽量把递归写成尾递归的方式，编译器会自动优化为循环，这里就不展开介绍了。

一般来说，递归这种方式于循环相比被认为是更符合人的思维的，即告诉机器做什么，而不是告诉机器怎么做。递归还是有很强大的表现力的，比如换零钱问题。

问题：假设某国的货币有若干面值，现给一张大面值的货币要兑换成零钱，问有多少种兑换方式。

递归解法：

def countChange(money: Int, coins: List[Int]): Int = { 
  if (money == 0) 
    1 
  else if (coins.size == 0 || money < 0) 
    0 
  else 
    countChange(money, coins.tail) + countChange(money - coins.head, coins) 
}

（示例来源：有趣的 Scala 语言: 使用递归的方式去思考）
从这个例子可以看出，函数式程序非常简练，描述做什么，而不是怎么做。

函数式语言当然还少不了以下特性：

高阶函数（Higher-order function）
偏应用函数（Partially Applied Functions）
柯里化（Currying）
闭包（Closure）

高阶函数就是参数为函数或返回值为函数的函数。有了高阶函数，就可以将复用的粒度降低到函数级别，相对于面向对象语言，复用的粒度更低。

举例来说，假设有如下的三个函数，

def sumInts(a: Int, b: Int): Int =
  if (a > b) 0 else a + sumInts(a + 1, b)

def sumCubes(a: Int, b: Int): Int =
  if (a > b) 0 else cube(a) + sumCubes(a + 1, b)

def sumFactorials(a: Int, b: Int): Int =
  if (a > b) 0 else fact(a) + sumFactorials(a + 1, b)

分别是求a到b之间整数之和，求a到b之间整数的立方和，求a到b之间整数的阶乘和。

其实这三个函数都是以下公式的特殊情况

sum_{n=a}^{b}{f(n)}

三个函数不同的只是其中的f不同，那么是否可以抽象出一个共同的模式呢？

我们可以定义一个高阶函数sum：

def sum(f: Int => Int, a: Int, b: Int): Int =
  if (a > b) 0
  else f(a) + sum(f, a + 1, b)

其中参数f是一个函数，在函数中调用f函数进行计算，并进行求和。

然后就可以写如下的函数

def sumInts(a: Int, b: Int) = sum(id, a, b)
def sumCubs(a: Int, b: Int) = sum(cube, a, b)
def sumFactorials(a: Int, b: Int) = sum(fact, a, b)

def id(x: Int): Int = x
def cube(x: Int): Int = x * x * x
def fact(x: Int): Int = if (x == 0) 1 else fact(x - 1)

这样就可以重用sum函数来实现三个函数中的求和逻辑。
（示例来源：https://d396qusza40orc.cloudfront.net/progfun/lecture_slides/week2-2.pdf）

高阶函数提供了一种函数级别上的依赖注入（或反转控制）机制，在上面的例子里，sum函数的逻辑依赖于注入进来的函数的逻辑。很多GoF设计模式都可以用高阶函数来实现，如Visitor，Strategy，Decorator等。比如Visitor模式就可以用集合类的map()或foreach()高阶函数来替代。

函数式语言通常提供非常强大的集合类（Collection），提供很多高阶函数，因此使用非常方便。

比如说，我们想对一个列表中的每个整数乘2，在命令式编程中需要通过循环，然后对每一个元素乘2，但是在函数式编程中，我们不需要使用循环，只需要使用如下代码：

scala> val numbers = List(1, 2, 3, 4)
numbers: List[Int] = List(1, 2, 3, 4)

scala> numbers.map(x=>x*2)
res3: List[Int] = List(2, 4, 6, 8)

（示例来源：Programming Scala: Tackle Multi-Core Complexity on the Java Virtual Machine一书的Introduction）

其中x=>x2是一个匿名函数，接收一个参数x，输出x2。这里也可以看出来函数式编程关注做什么（x*2），而不关注怎么做（使用循环控制结构）。程序员完全不关心，列表中的元素是从前到后依次计算的，还是从后到前依次计算的，是顺序计算的，还是并行进行的计算，如Scala的并行集合（Parallel collection）。

使用集合类的方法，可以使对一些处理更简单，例如上面提到的求阶乘的函数，如果使用集合类，就可以写成：

def fact(n: Int): Int = (1 to n).reduceLeft((acc,k)=>acc*k)

其中(1 to n)生成一个整数序列，而reduceLeft()高阶函数通过调用匿名函数将序列化简。

那么，在大数据处理框架Spark中，一个RDD就是一个集合。以词频统计的为例代码如下：

val file = spark.textFile("hdfs://...")
val counts = file.flatMap(line => line.split(" "))
                 .map(word => (word, 1))
                 .reduceByKey(_ + _)
counts.saveAsTextFile("hdfs://...")

（示例来源：https://spark.apache.org/examples.html）

示例里的flatMap()，map()，和集合类中的同名方法是一致的，这里的map方法的参数也是一个匿名函数，将单词变成一个元组。写这个函数的人不用关心函数是怎么调度的，而实际上，Spark框架会在多台计算机组成的分布式集群上完成这个计算。

此外，如果对比一下Hadoop的词频统计实现：WordCount - Hadoop Wiki ，就可以看出函数式编程的一些优势。

函数式编程语言还提供惰性求值（Lazy evaluation，也称作call-by-need），是在将表达式赋值给变量（或称作绑定）时并不计算表达式的值，而在变量第一次被使用时才进行计算。这样就可以通过避免不必要的求值提升性能。在Scala里，通过lazy val来指定一个变量是惰性求值的，如下面的示例所示：

scala> val x = { println("x"); 15 }
x
x: Int = 15

scala> lazy val y = { println("y"); 13 }
y: Int = <lazy>

scala> y
y
res3: Int = 13

scala> y
res4: Int = 13

（示例来源：scala - What does a lazy val do?）

可以看到，在Scala的解释器中，当定义了x变量时就打印出了“x”，而定义变量y时并没有打印出”y“，而是在第一次引用变量y时才打印出来。

函数式编程语言一般还提供强大的模式匹配（Pattern Match）功能。在函数式编程语言中可以定义代数数据类型（Algebraic data type），通过组合已有的数据类型形成新的数据类型，如在Scala中提供case class，代数数据类型的值可以通过模式匹配进行分析。

总结

函数式编程是给软件开发者提供的另一套工具箱，为我们提供了另外一种抽象和思考的方式。

函数式编程也有不太擅长的场合，比如处理可变状态和处理IO，要么引入可变变量，要么通过Monad来进行封装（如State Monad和IO Monad）